Bealekoderne, og hvorfor de kan være svære at bryde
 Dette
er ikke en general artikel om kodning af tekster. Dem findes der allerede mange
af på nettet, og de er skrevet af mennesker, der ved langt mere om emnet
end jeg gør. Artiklen er skrevet med udgangspunkt i min artikel om
Beales Skat og koderne, der er relateret til dette
dokument, og primært foranlediget af, at nogle af fortalerne for, at hele
historien om skatten er et falsum, og koderne derfor er "falske" og ikke reelt
skjuler en meningsfuld tekst, bruger som argument, at når koderne endnu ikke er
brudt, selv ikke med anvendelse af moderne computerteknologi, er det fordi de
ikke kan brydes, og når de ikke kan brydes, er det altså fordi, de ikke i
virkeligheden dækker
over noget meningsfyldt. Jeg hører selv til skeptikerne omkring "skattesagen",
men er ikke enig i, at Beale ikke kunne konstruere en kode, der vol være meget
svær at bryde, selv med moderne hjælpemidler, uden at man har adgang til nøglen.
Dette
er ikke en general artikel om kodning af tekster. Dem findes der allerede mange
af på nettet, og de er skrevet af mennesker, der ved langt mere om emnet
end jeg gør. Artiklen er skrevet med udgangspunkt i min artikel om
Beales Skat og koderne, der er relateret til dette
dokument, og primært foranlediget af, at nogle af fortalerne for, at hele
historien om skatten er et falsum, og koderne derfor er "falske" og ikke reelt
skjuler en meningsfuld tekst, bruger som argument, at når koderne endnu ikke er
brudt, selv ikke med anvendelse af moderne computerteknologi, er det fordi de
ikke kan brydes, og når de ikke kan brydes, er det altså fordi, de ikke i
virkeligheden dækker
over noget meningsfyldt. Jeg hører selv til skeptikerne omkring "skattesagen",
men er ikke enig i, at Beale ikke kunne konstruere en kode, der vol være meget
svær at bryde, selv med moderne hjælpemidler, uden at man har adgang til nøglen.
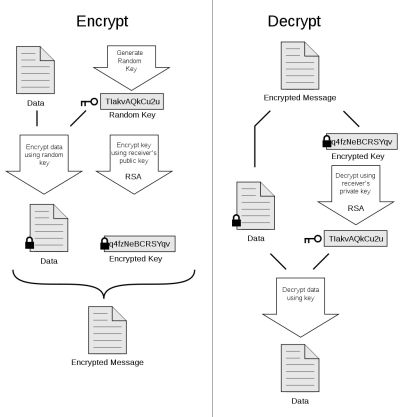
I dag er det ved hjælp af krypteringsalgoritmer muligt at lave koder, der er i praksis umulige at bryde, alene fordi det vil krævede uanede mængder af computerkraft og utroligt lang tid. Et eksempel på sådanne algoritmer er de såkaldte PGP algoritmer, som i sin tid blev udviklet af amerikaneren Phil Zimmermann i 1991. Der er i dag tale om en såkaldt "assymetrisk" kode*, hvor indkodning og afkodning foregår ved hjælp af to forskellige nøgler, og man skal altså kende dem begge, for at kunne "knække koden". Et eksempel (på engelsk) på, hvordan en sådan asymmetrisk kode virker, kan ses i illustrationen til højre. Når der indkodes genereres en tilfældig nøgle, som indkodningen sker ved hjælp af. Når teksten sendes, indkodes nøglen med det, der kaldes "modtagerens offentlige nøgle". Derefter sendes både selve de krypterede data og den krypterede nøgle til modtageren. Modtageren starter med at dekryptere nøglen med sin private nøgle, og derefter dekrypteres teksten med den tilsendte nøgle. Vupti! Så er dokumentet tilbage, som det oprindeligt var. Hvis en person, der ikke er den rigtige modtager, skal bryde koden, skal vedkommende altså kende både modtagerens offentlige og private nøgle, og det er ret tvivlsomt at det kan ske, eller også skal der bruges såkaldt "brute force", hvor en computer simpelthen "prøver sig frem" med at erstatte kodesymbolerne med tegn, og så se om disse giver mening. Da der mange gange kan komme mange eksisterende ord og sætninger ud af en sådan "brute force", er computeren eller de, der betjener den,også nødt til at kunne forstå sammenhængen, for at de om en løsning er rigtig. Og det er det, der tager tiden. PGP koden blev betragtet så sikker, at da koden blev kendt og brugt uden for USA, sigtede National Security Agency (NSA) Zimmermann for at "eksportere krigsmaterial uden tillaldelse", da fjendtlige magter kunne anvende koden, og NSA ikke kunne bryde den. Sagen endte dog uden at Zimmermann blev anklaget. Dengang blev nøgler, der var længere end 40 bits betragtet som krigsmateriel, og Zimmernans nøgle var 128 bits. Zimmermann offentliggjorde imidlertid kildekoden til sin algoritme, og ås var den jo ikke mere hemmelig. Selv om der i dag anvendes en endnu længere nøgle, er reglerne lempet, og PGP og tilsvarende algoritmer betragtes ikke længere som krigsmateriel (bortset fra, hvis det sælges til en række specifikke lande).
* Da Zimmermann udviklede algoritmen, var den symmetrisk. Det vil sige at den blev ind- og afkodet ved hjælp af samme nøgle, og man skulle altså kun kende denne, for at kunne bryde koden.
Allerede tilbage i 1980'erne, altså før PGP, talt man om koder, der var så komplicerede (2048 bits), at selv med verdens dengang hurtigste computer ville det tage - og hold nu godt fast- 15 gange så lang tid som universet havde eksisteret, at bryde koden ved hjælp af "brute force", og sådanne koder blev derfor betragtet som ubrydelige. Siden er computerne selvfølgelig blevet forbedret kraftigt, men det samme er algoritmerne.
Disse muligheder havde man imidlertid ikke i begyndelsen af det 19. århundrede, hvor Beale koderne angiveligt blev forfattet, og selv om nogle af de andre teorier om skatten skulle være sande, og koderne derfor først skrevet senere i århundredet, var forholdende de samme, da der fortsat ikke eksisterede maskiner til at foretage indkodning, så det skulle under alle omstændigheder ske manuelt. Men hvis koderne er oprettet manuel, og vi forudsætter, at de er ægte og ikke bare tilfældige tal, som nogle forskere mener, hvorfor kan en supercomputer, så ikke bryde dem? Det vil jeg prøve at se nærmere på i det følgende. Men lad mig starte med at se lidt på "manuel kodning" i almindelighed.
Kodeskrift
Kodeskrift har eksisteret i flere tusinde år. En kendt cifferkode er den såkaldte Cæsarkode, eller Cæsaralgoritme, fordi den blev benyttet under Julius Cæsar. Det er en såkaldt monoalfabetisk subsitutionsalgoritme, og selv om navnet kan lyde fancy, er det egentlig en forholdsvis nem algoritme både at kode og indkode, da den simpelthen er baseret på at et tegn i alfabetet erstattes af et andet efter et bestemt system. Mit navn "Jan Kronsell" bliver til (med en nøgle på +4), hvor hvert bogstav erstattes af fire bogstaver længere henne i alfabetet): "ner ovsrwipp". Det kan selvfølgelig gøres lidt sværere ved at undlade at dele koden op i ord, som originalteksten, men ikke meget sværere, og koder af denne type brydes ret nemt ved hjælp af frekvensanalyse (mere om dette nedenfor), hvilket faktisk gælder de fleste substitutionskoder.
Vanskeligere bliver det dog, hvis man anvender såkaldt polyalfabetiske koder, hvor der anvendes flere alfabeter med forskellig forskydning, så det samme bogstav i klarteksten, ikke oversættes til det samme bogstav, hver gang man møder det. Det betyder, at mange bogstaver "oversættes" til det samme bogstav, mens samme bogstav kan få flere forskellige værdier. Det gør frekvensanalyse vanskeligere - men ikke umulig. Jo flere alfabeter koden er baseret på, jo vanskeligere bliver det selvfølgelig. Og der kan laves substitutionskoder, baseret på nøgler, som gør det endnu sværere. Her kunne man fx aftale (som nøgle) at der skiftes alfabet for hver femte bogstav eller lignende, som vil skabe netop en struktur, som vil være vanskelig at frekvensanalysere. Her er mit navn oversat med tre alfabeter, og der skiftes alfabet for hvert andet bogstav: "ner saærwmtx". Læg mærke til, at de to n'er i navnet tilfældigvis begge oversættes til 'r', mens de to to l'er oversættes til henholdsvis 't' og 'x'. De tre anvendte alfabeter er alle forskudt med en faktor fire, men jeg kunne også have valgt at lade dem forskyde med forskellige faktorer -og have brugt forskellige alfabeter for hvert bogstav, som i dette eksempel, hvor der er anvendt tre forskellige alfabeter med forskydninger på hhv. 20, 0 og 13, og så bliver "Jan" til "aaa", og tre ens bogstaver kan jo oversættes til hvad som helst, men det er ikke svært, hvis man har nøglen. En computer ville have meget vanskeligt ved at bryde en sådan kode, da den dels er meget kort, og da de tre bogstaver, kan repræsentere alle eksisterende ord på tre bogstaver. Computeren vil selvfølgelig nå frem til "Jan" blandt mulighederne, men også "kan", "han", "vil", "til", "mil" og så videre, så hvis den, der skal læse resultatet ikke ved mere, vil løsningen være meningsløs. Også betydningen af kodens længde, vender jeg tilbage til nedenfor.
Man kan også gøre det sværere at bryde koden, ved at bruge multikodning - altså først kode originalteksten med en kode, og kode koden med en anden kode og så fremdeles. Her er mit navn efter dette system: "eee fvfiwygp". Først er navnet indkodet med den den monoalfabetiske kode med forskydning 4, som jeg beskrev i første afsnit, dernæst med den ovenstående med tre alfabeter og skift for hvert bogstav.
 En
metode, der blev brugt under 2. Verdenskrig til kommunikation mellem de briterne
og de danske modstandsfolk, blev beskrevet af Flemming B. Muus, faldskærmschef
under besættelsen, i romanen "Der kom en dag" fra 1953. Muus blev senere (efter
krigen) dømt for bedrageri mod modstandsbevægelsen, men det har ikke noget med
denne sag at gøre. Koden, som man benyttede, var baseret på det engelske
alfabet, altså uden bogstaverne Æ, Ø og Å. De 26 bogstaver skulle nu indskrives
i et kvadrat på 25 * 25 felter i det 'i' og 'j' stod i samme kvadrat. Der skulle
nu bruges en nøgle (eller et kodeord), som skulle indskrives i kvadratets første felter, dog
således at bogstaver, der gik igen, kun blev indskrevet første gang. De øvrige
felter blev så fyldt ud med resten af alfabetets bogstaver. I romanen anvender Muus som
nøgle, omanens titel, og det giver det kvadrat, der er vist i
figuren til venstre.
En
metode, der blev brugt under 2. Verdenskrig til kommunikation mellem de briterne
og de danske modstandsfolk, blev beskrevet af Flemming B. Muus, faldskærmschef
under besættelsen, i romanen "Der kom en dag" fra 1953. Muus blev senere (efter
krigen) dømt for bedrageri mod modstandsbevægelsen, men det har ikke noget med
denne sag at gøre. Koden, som man benyttede, var baseret på det engelske
alfabet, altså uden bogstaverne Æ, Ø og Å. De 26 bogstaver skulle nu indskrives
i et kvadrat på 25 * 25 felter i det 'i' og 'j' stod i samme kvadrat. Der skulle
nu bruges en nøgle (eller et kodeord), som skulle indskrives i kvadratets første felter, dog
således at bogstaver, der gik igen, kun blev indskrevet første gang. De øvrige
felter blev så fyldt ud med resten af alfabetets bogstaver. I romanen anvender Muus som
nøgle, omanens titel, og det giver det kvadrat, der er vist i
figuren til venstre.
Den tekst, der skulle indkodes, blev nu opdelt i grupper på to bogstavet. Mit navn ville derfor blive til 'ja nk ro ns el lx" idet et manglende bogstav blev erstattet af et 'x'. Nu finder man så de to bogstaver i kvadratet. Fx står 'j/i' i tredje række, fjerde kolonne, mens 'a' står i anden række, tredje kolonne. Man finder nu de bogstaver, der stod i modsatte hjørner af det fundne kvadrat, altså her 'h' og 'g'. Da 'J' er det første bogstav i den tekst, der skal indkodes, bliver koden 'hg'. Havde det været 'aj', der skulle indkodes, var løsningen blevet 'gh'. Står de to bogstaver i samme række eller kolonne, som fx 'r' og 'o', tages bogstaverne lige efter disse (her 'k' og 'd', idet der startes forfra på rækken, hvis man "ryger ud over sidste kolonne. Tilsvarende gør man, hvis bogstaverne står i samme kolonne. Mit navn ville således blive til "hg eg kd aq of hz", som så kan skrives uden grupperingen som "hgegkdaqofhz", som selv ved længere tekster, ville vanskeliggøre frekvensanalyse, da det dels ikke er indlysende, at bogstaverne "hænger sammen" to og to, og samme bogstav repræsenterer forskellige værdier; fx repræsenterer det første 'g' et 'a', men det næste 'g' repræsenterer et 'n', og ved længere tekster bliver tendensen endnu mere tydelig. Skulle den samme metode bruges mange gange, kunne man skifte nøglen i begyndelsen ud, men det krævede jo, at man kunne kommunikere den nye lnøglr til modtagerne. Dette kunne undr besættelsen gøres ved radioudsendelserne fra London, hvor de enkelte modstandsgrupper så vidste, at når der var "Hilsen til Bjarne Elias og Morten", så var det næste budskab til dem, og dette kunne så fx være en ny sætning: "Haaber ferien var god", som ville give et nyt kvadrat med deraf følgende nye oversættelser. mit nasvn bliver med denne kodesætning til "djvchlqrkcz""; altså radikalt anderledes end med den første kode. Heller ikke en kode af denne art er naturligvis ubrydelig, men gør det mere besværligt, ikke mindst hvis man ikke gennemskuer systemet med opdeling i grupper af to. Beale behøvede ingen radiokommukation. da han jo ville sende nøglen til Morriss i et brev, så han kunne i princippet bruge så mange kvadrater som han havde lyst til, skrive dem i brevet, og fortælle om, hvordan og hvor oefte, Morriss skulle skifte mellem disse ved dechifreringen. Fx kunne han lave 10 forskellige alfabetkvadrater og skifte for hver sætning eller hvert ord, inden han så kodede den volapyktekst, der kom ud af med en tal, der repræsenterede bogstaver fra en bog.
Med computere kan der genereres langt mere komplicerede koder, som fx med RSA systemet, opkaldt efter initialerne på de tre matematikere, der fandt på systemet i sin tid (1977), som er en forgænger for ovennævnte PDP, som i virkeligheden bare er en implementering af RSA. Som de fleste andre asymmetriske algoritmer, er såvel RSA som PGP baseret på anvendelsen af nogle meget store primtal. Men tilbage til de metoder, Beale og hans samtid kunne anvende.
Bealekoderne
 Hvis
historien er sand, efterlod T. J. Beale hos en Mr. Morriss, hvor han boede et
par gange i 1819 og 1821 et brev, der blandt andet indeholdt tre ark papir
beskrevet med tal. Dette kan man læse mere om i artiklen om Beales Skat, se link
ovenfor. Illustrationen til højre viser en afskrift fra den pamflet, der omtales
i min artikel om skatten. Afskriften viser det såkaldte dokument B3, som skulle
fortælle, hvem der havde krav på en andel af skatten, hvor de boede og hvem,
deres eventuelle efterkommere var. Som det fremgår indeholder dokumentet en
række tal, og det samme var tilfældet for de to andre dokumenter, der indeholder
henholdsvis en beskrivelse af skatten (B2) og hvor man kan finde den (B1).
Hvis
historien er sand, efterlod T. J. Beale hos en Mr. Morriss, hvor han boede et
par gange i 1819 og 1821 et brev, der blandt andet indeholdt tre ark papir
beskrevet med tal. Dette kan man læse mere om i artiklen om Beales Skat, se link
ovenfor. Illustrationen til højre viser en afskrift fra den pamflet, der omtales
i min artikel om skatten. Afskriften viser det såkaldte dokument B3, som skulle
fortælle, hvem der havde krav på en andel af skatten, hvor de boede og hvem,
deres eventuelle efterkommere var. Som det fremgår indeholder dokumentet en
række tal, og det samme var tilfældet for de to andre dokumenter, der indeholder
henholdsvis en beskrivelse af skatten (B2) og hvor man kan finde den (B1).
Her er tallene til koderne i en mere læsbar form:
B1
71, 194, 38,
1701, 89, 76, 11, 83, 1629, 48, 94, 63, 132, 16, 111, 95, 84, 341,
975, 14, 40, 64, 27, 81, 139, 213, 63, 90, 1120, 8, 15, 3, 126, 2018, 40, 74,
758, 485, 604, 230, 436, 664, 582, 150, 251, 284, 308, 231, 124, 211, 486, 225,
401, 370, 11, 101, 305, 139, 189, 17, 33, 88, 208, 193, 145, 1, 94, 73, 416,
918, 263, 28, 500, 538, 356, 117, 136, 219, 27, 176, 130, 10, 460, 25, 485, 18,
436, 65, 84, 200, 283, 118, 320, 138, 36, 416, 280, 15, 71, 224, 961, 44, 16,
401,
39, 88, 61, 304, 12, 21, 24, 283, 134, 92, 63, 246, 486, 682, 7, 219, 184, 360,
780,
18, 64, 463, 474, 131, 160, 79, 73, 440, 95, 18, 64, 581, 34, 69, 128, 367, 460,
17,
81, 12, 103, 820, 62, 116, 97, 103, 862, 70, 60, 1317, 471, 540, 208, 121, 890,
346, 36, 150, 59, 568, 614, 13, 120, 63, 219, 812, 2160, 1780, 99, 35, 18, 21,
136,
872, 15, 28, 170, 88, 4, 30, 44, 112, 18, 147, 436, 195, 320, 37, 122, 113, 6,
140,
8, 120, 305, 42, 58, 461, 44, 106, 301, 13, 408, 680, 93, 86, 116, 530, 82, 568,
9,
102, 38, 416, 89, 71, 216, 728, 965, 818, 2, 38, 121, 195, 14, 326, 148, 234,
18,
55, 131, 234, 361, 824, 5, 81, 623, 48, 961, 19, 26, 33, 10, 1101, 365, 92, 88,
181,
275, 346, 201, 206, 86, 36, 219, 324, 829, 840, 64, 326, 19, 48, 122, 85, 216,
284,
919, 861, 326, 985, 233, 64, 68, 232, 431, 960, 50, 29, 81, 216, 321, 603, 14,
612,
81, 360, 36, 51, 62, 194, 78, 60, 200, 314, 676, 112, 4, 28, 18, 61, 136, 247,
819,
921, 1060, 464, 895, 10, 6, 66, 119, 38, 41, 49, 602, 423, 962, 302, 294, 875,
78,
14, 23, 111, 109, 62, 31, 501, 823, 216, 280, 34, 24, 150, 1000, 162, 286, 19,
21,
17, 340, 19, 242, 31, 86, 234, 140, 607, 115, 33, 191, 67, 104, 86, 52, 88, 16,
80,
121, 67, 95, 122, 216, 548, 96, 11, 201, 77, 364, 218, 65, 667, 890, 236, 154,
211,
10, 98, 34, 119, 56, 216, 119, 71, 218, 1164, 1496, 1817, 51, 39, 210, 36, 3,
19,
540, 232, 22, 141, 617, 84, 290, 80, 46, 207, 411, 150, 29, 38, 46, 172, 85,
194,
39, 261, 543, 897, 624, 18, 212, 416, 127, 931, 19, 4, 63, 96, 12, 101, 418, 16,
140,
230, 460, 538, 19, 27, 88, 612, 1431, 90, 716, 275, 74, 83, 11, 426, 89, 72, 84,
1300, 1706, 814, 221, 132, 40, 102, 34, 868, 975, 1101, 84, 16, 79, 23, 16, 81,
122,
324, 403, 912, 227, 936, 447, 55, 86, 34, 43, 212, 107, 96, 314, 264, 1065, 323,
428, 601, 203, 124, 95, 216, 814, 2906, 654, 820, 2, 301, 112, 176, 213, 71, 87,
96,
202, 35, 10, 2, 41, 17, 84, 221, 736, 820, 214, 11, 60, 760.
B2
115, 73, 24,
807, 37, 52, 49, 17, 31, 62, 647, 22, 7, 15, 140, 47, 29, 107, 79, 84,
56, 239, 10, 26, 811, 5, 196, 308, 85, 52, 160, 136, 59, 211, 36, 9, 46, 316,
554,
122, 106, 95, 53, 58, 2, 42, 7, 35, 122, 53, 31, 82, 77, 250, 196, 56, 96, 118,
71,
140, 287, 28, 353, 37, 1005, 65, 147, 807, 24, 3, 8, 12, 47, 43, 59, 807, 45,
316,
101, 41, 78, 154, 1005, 122, 138, 191, 16, 77, 49, 102, 57, 72, 34, 73, 85, 35,
371,
59, 196, 81, 92, 191, 106, 273, 60, 394, 620, 270, 220, 106, 388, 287, 63, 3, 6,
191, 122, 43, 234, 400, 106, 290, 314, 47, 48, 81, 96, 26, 115, 92, 158, 191,
110,
77, 85, 197, 46, 10, 113, 140, 353, 48, 120, 106, 2, 607, 61, 420, 811, 29, 125,
14,
20, 37, 105, 28, 248, 16, 159, 7, 35, 19, 301, 125, 110, 486, 287, 98, 117, 511,
62,
51, 220, 37, 113, 140, 807, 138, 540, 8, 44, 287, 388, 117, 18, 79, 344, 34, 20,
59,
511, 548, 107, 603, 220, 7, 66, 154, 41, 20, 50, 6, 575, 122, 154, 248, 110, 61,
52, 33,
30, 5, 38, 8, 14, 84, 57, 540, 217, 115, 71, 29, 84, 63, 43, 131, 29, 138, 47,
73, 239,
540, 52, 53, 79, 118, 51, 44, 63, 196, 12, 239, 112, 3, 49, 79, 353, 105, 56,
371, 557,
211, 505, 125, 360, 133, 143, 101, 15, 284, 540, 252, 14, 205, 140, 344, 26,
811, 138,
115, 48, 73, 34, 205, 316, 607, 63, 220, 7, 52, 150, 44, 52, 16, 40, 37, 158,
807, 37,
121, 12, 95, 10, 15, 35, 12, 131, 62, 115, 102, 807, 49, 53, 135, 138, 30, 31,
62, 67, 41,
85, 63, 10, 106, 807, 138, 8, 113, 20, 32, 33, 37, 353, 287, 140, 47, 85, 50,
37, 49, 47,
64, 6, 7, 71, 33, 4, 43, 47, 63, 1, 27, 600, 208, 230, 15, 191, 246, 85, 94,
511, 2, 270,
20, 39, 7, 33, 44, 22, 40, 7, 10, 3, 811, 106, 44, 486, 230, 353, 211, 200, 31,
10, 38,
140, 297, 61, 603, 320, 302, 666, 287, 2, 44, 33, 32, 511, 548, 10, 6, 250, 557,
246,
53, 37, 52, 83, 47, 320, 38, 33, 807, 7, 44, 30, 31, 250, 10, 15, 35, 106, 160,
113, 31,
102, 406, 230, 540, 320, 29, 66, 33, 101, 807, 138, 301, 316, 353, 320, 220, 37,
52,
28, 540, 320, 33, 8, 48, 107, 50, 811, 7, 2, 113, 73, 16, 125, 11, 110, 67, 102,
807, 33,
59, 81, 158, 38, 43, 581, 138, 19, 85, 400, 38, 43, 77, 14, 27, 8, 47, 138, 63,
140, 44,
35, 22, 177, 106, 250, 314, 217, 2, 10, 7, 1005, 4, 20, 25, 44, 48, 7, 26, 46,
110, 230,
807, 191, 34, 112, 147, 44, 110, 121, 125, 96, 41, 51, 50, 140, 56, 47, 152,
540,
63, 807, 28, 42, 250, 138, 582, 98, 643, 32, 107, 140, 112, 26, 85, 138, 540,
53, 20,
125, 371, 38, 36, 10, 52, 118, 136, 102, 420, 150, 112, 71, 14, 20, 7, 24, 18,
12, 807,
37, 67, 110, 62, 33, 21, 95, 220, 511, 102, 811, 30, 83, 84, 305, 620, 15, 2,
108, 220,
106, 353, 105, 106, 60, 275, 72, 8, 50, 205, 185, 112, 125, 540, 65, 106, 807,
188, 96, 110,
16, 73, 33, 807, 150, 409, 400, 50, 154, 285, 96, 106, 316, 270, 205, 101, 811,
400, 8,
44, 37, 52, 40, 241, 34, 205, 38, 16, 46, 47, 85, 24, 44, 15, 64, 73, 138, 807,
85, 78, 110,
33, 420, 505, 53, 37, 38, 22, 31, 10, 110, 106, 101, 140, 15, 38, 3, 5, 44, 7,
98, 287,
135, 150, 96, 33, 84, 125, 807, 191, 96, 511, 118, 40, 370, 643, 466, 106, 41,
107,
603, 220, 275, 30, 150, 105, 49, 53, 287, 250, 208, 134, 7, 53, 12, 47, 85, 63,
138, 110,
21, 112, 140, 485, 486, 505, 14, 73, 84, 575, 1005, 150, 200, 16, 42, 5, 4, 25,
42,
8, 16, 811, 125, 160, 32, 205, 603, 807, 81, 96, 405, 41, 600, 136, 14, 20, 28,
26,
353, 302, 246, 8, 131, 160, 140, 84, 440, 42, 16, 811, 40, 67, 101, 102, 194,
138,
205, 51, 63, 241, 540, 122, 8, 10, 63, 140, 47, 48, 140, 288.
B3
317, 8, 92, 73, 112, 89, 67, 318, 28, 96, 107,
41, 631, 78, 146, 397, 118, 98,
114, 246, 348, 116, 74, 88, 12, 65, 32, 14, 81, 19, 76, 121, 216, 85, 33, 66,
15,
108, 68, 77, 43, 24, 122, 96, 117, 36, 211, 301, 15, 44, 11, 46, 89, 18, 136,
68,
317, 28, 90, 82, 304, 71, 43, 221, 198, 176, 310, 319, 81, 99, 264, 380, 56, 37,
319, 2, 44, 53, 28, 44, 75, 98, 102, 37, 85, 107, 117, 64, 88, 136, 48, 154, 99,
175,
89, 315, 326, 78, 96, 214, 218, 311, 43, 89, 51, 90, 75, 128, 96, 33, 28, 103,
84,
65, 26, 41, 246, 84, 270, 98, 116, 32, 59, 74, 66, 69, 240, 15, 8, 121, 20, 77,
89,
31, 11, 106, 81, 191, 224, 328, 18, 75, 52, 82, 117, 201, 39, 23, 217, 27, 21,
84,
35, 54, 109, 128, 49, 77, 88, 1, 81, 217, 64, 55, 83, 116, 251, 269, 311, 96,
54, 32,
120, 18, 132, 102, 219, 211, 84, 150, 219, 275, 312, 64, 10, 106, 87, 75, 47,
21,
29, 37, 81, 44, 18, 126, 115, 132, 160, 181, 203, 76, 81, 299, 314, 337, 351,
96, 11,
28, 97, 318, 238, 106, 24, 93, 3, 19, 17, 26, 60, 73, 88, 14, 126, 138, 234,
286,
297, 321, 365, 264, 19, 22, 84, 56, 107, 98, 123, 111, 214, 136, 7, 33, 45, 40,
13,
28, 46, 42, 107, 196, 227, 344, 198, 203, 247, 116, 19, 8, 212, 230, 31, 6, 328,
65, 48, 52, 59, 41, 122, 33, 117, 11, 18, 25, 71, 36, 45, 83, 76, 89, 92, 31,
65, 70,
83, 96, 27, 33, 44, 50, 61, 24, 112, 136, 149, 176, 180, 194, 143, 171, 205,
296,
87, 12, 44, 51, 89, 98, 34, 41, 208, 173, 66, 9, 35, 16, 95, 8, 113, 175, 90,
56,
203, 19, 177, 183, 206, 157, 200, 218, 260, 291, 305, 618, 951, 320, 18, 124,
78,
65, 19, 32, 124, 48, 53, 57, 84, 96, 207, 244, 66, 82, 119, 71, 11, 86, 77, 213,
54,
82, 316, 245, 303, 86, 97, 106, 212, 18, 37, 15, 81, 89, 16, 7, 81, 39, 96, 14,
43,
216, 118, 29, 55, 109, 136, 172, 213, 64, 8, 227, 304, 611, 221, 364, 819, 375,
128, 296, 1, 18, 53, 76, 10, 15, 23, 19, 71, 84, 120, 134, 66, 73, 89, 96, 230,
48,
77, 26, 101, 127, 936, 218, 439, 178, 171, 61, 226, 313, 215, 102, 18, 167, 262,
114, 218, 66, 59, 48, 27, 19, 13, 82, 48, 162, 119, 34, 127, 139, 34, 128, 129,
74,
63, 120, 11, 54, 61, 73, 92, 180, 66, 75, 101, 124, 265, 89, 96, 126, 274, 896,
917,
434, 461, 235, 890, 312, 413, 328, 381, 96, 105, 217, 66, 118, 22, 77, 64, 42,
12,
7, 55, 24, 83, 67, 97, 109, 121, 135, 181, 203, 219, 228, 256, 21, 34, 77, 319,
374,
382, 675, 684, 717, 864, 203, 4, 18, 92, 16, 63, 82, 22, 46, 55, 69, 74, 112,
134,
186, 175, 119, 213, 416, 312, 343, 264, 119, 186, 218, 343, 417, 845, 951, 124,
209, 49, 617, 856, 924, 936, 72, 19, 28, 11, 35, 42, 40, 66, 85, 94, 112, 65,
82,
115, 119, 236, 244, 186, 172, 112, 85, 6, 56, 38, 44, 85, 72, 32, 47, 63, 96,
124,
217, 314, 319, 221, 644, 817, 821, 934, 922, 416, 975, 10, 22, 18, 46, 137, 181,
101,39, 86, 103, 116, 138, 164, 212, 218, 296, 815, 380, 412, 460, 495, 675,
820,
952.
Den ukendte forfatter til den pamflet, hvor koderne fandtes, havde efter mange års forsøg lykkedes med at oversætte indholdet af B2. Af tallene fremgår, at det ikke kan være en simpel alfabetisk substitution, dertil er der for mange og for høje tal. I den periode, der er tale om, var det almindeligt at indkode tekster i henhold til bøger eller andre skrifter, som man havde, og som man kunne forvente at modtageren også havde adgang til. Det er da også det, forfatteren havde gjort. Han fandt ud af, at B2 var indkodet med den amerikanske Uafhængighedserklæring, og han oversatte dens indhold til
”I have deposited in the county of Bedford, about four miles from Buford's, in an excavation or vault, six feet below the surface of the ground, the following articles, belonging jointly to the parties whose names are given in number "3," herewith:
The first deposit consisted of one thousand and fourteen pounds of gold, and three thousand eight hundred and twelve pounds of silver, deposited November, 1819. The second was made December, 1821, and consisted of nineteen hundred and seven pounds of gold, and twelve hundred and eighty-eight pounds of silver; also jewels, obtained in St. Louis in exchange for silver to save transportation, and valued at $13,000.
The above is securely packed in iron pots, with iron covers. The vault is roughly lined with stone, and the vessels rest on solid stone, and are covered with others. Paper number "1" describes the exact locality of the vault so that no difficulty will be had in finding it”.
På dansk i min egen oversættelse bliver dette til
I Bedford County, omkring fire miles (ca. 6,5 km) fra Buford’s, har jeg, i en udgravning eller hvælving, seks fod under overfladen, deponeret følgende artikler, der i forening tilhører de personer, der er nævnt i nummer 3:
Den første deponering bestod af et tusinde og fjorten pund guld og tre tusinde ottehundrede og tolv pund sølv, deponeret i november 1819. Den anden blev gjort i december 1821 og bestod af nitten hundrede og syv pund guld, og tolvhundrede otteogfirs pund sølv; desuden juveler, anskaffet i St. Louis i bytte for sølv for at spare transport, til en værdi af $13.000
Ovenstående er forsvarligt pakket i jerntønder med jernlåg. Hvælvingen er groft beklædt med sten, og beholderne hviler på massiv sten og er dækket af andre sten. Papir nummer 1 beskriver hvælvingens præcise placering, så den kan genfindes uden problemer.
For at nå frem til dette resultat, skal man ikke bruge en standardversion af Uafhængighedserklæringen, men en sådan fandtes faktisk heller ikke i 1820, hvor der eksisterede mindst 350 versioner af denne. Forskellene mellem de enkelte versioner var nok subtile, men store nok til at valgte man den forkerte version, blev koden "volapyk", når den blev oversat. Som det fremgår af artiklen om skatten, er det faktisk lykkedes at få en computer til at bryde denne kode og opnå det samme resultat (med en fejlprocent på 5), uden at computeren havde nøglen. Derimod er det aldrig lykkedes, hverken for computere eller manuelt, at bryde koderne i B1 og B3, selv om enkelte påstår, at de har gjort det, men de fortæller sjældent hvordan. En enkelt der påstår at have brudt koden i B3, har strakt elastikken langt, for at få koden til at "gå op". Hvis ikke de to andre koder er "falske" har dette været den nemmeste at bryde uden nøgle, og jeg ville nok også selv have valgt at bruge mindst tid på denne, da den jo ikke fortæller noget afgørende om, hvor skatten findes, og så brugt meget mere tid på ikke mindst B1, som netop afslører placeringen, og i lidt mindre grad på B3, som skulle sikre "arvingerne" anonymitet.
Men kunne man dengang lave en kode, der var så stærk, at selv moderne dages computere, ville få problemer med at bryde den? Efter min mening, ja, men det ville have krævet en del anstrengelser.
Frekvensanalyse
Et af de værktøjer, man bruger. når man skal bryde koder, er frekvensanalyse, og det er typisk også den måde en computeralgoritme vil gribe sagen an. En frekvensanalyse bygger på det faktum, at ikke alle alfabetets bogstaver bruges lige meget i et givent sprog. På dansk er det mest anvendte bogstav 'e', som bruges i omkring 16 % af alle ord. Dernæst følger 'r' , 'n', 'd' og 't' alle med mellem 7 og 8 %. Da brugen varierer i forskellige tekster, deler man typisk bogstaverne ind i nogle grupper:
E,
R T N,
I A D S O,
L G K V M F,
P U B H Æ Y,
Å Ø J C W og
X Z Q.
Desuden ser man på bogstaver, der typisk forekommer parvis og med tre i samme rækkefølge, fx ER DE EN ET GE RE TE TI og DET DEN ERE DER. På baggrund af frekvenserne, og grupperne, kan man så analyserer koderne, og se, om der er tegn, tal eller symboler i disse, som giver tilsvarende resultater. Er der fx et tegn, som udgør 14,3 procent af alle tegn, er der en god grund til at tro, at dette symbol repræsenterer 'e', og så fremdeles. På engelsk er fordelingen anturligvis anderledes end ovenstående, der er den, der gælder på dansk.I dette afsnit (til og med ordet "dansk", udgør 'e' godt 20 %, 'r' 11 % og 'd' og 'n' hver 7 % så det passer fint med den generelle fordeling. Det andet afsnit i artiklen; det der starter med "I dag er det.." og slutter med "...en række specifikke lande." har en fordeling, hvor 'e' udgør 16,8 procent, 'n' og 'r' henholdsvis 8,1 og 7,9 procent og 'd' 6,9 %, så igen passer det fint med det forventede, faktisk bedre end i det første eksempel, hvilket skyldes at teksten er længere, for jo længere en tekst er, jo mere præcis bliver frekvensanalysen. I den engelske tekst overfor (oversættelsen af B2) udgør 'e' 13 %, 'o' 8,7%, 't' og 'n' hver 8,33 % og 'i' 7 %. Bogstaver 'k' er kun brugt en eneste gang i den engelske tekst, mens to bogstaver 'q' og 'z' set ikke forekommer. Det harmonerer meget godt med den generelle fordeling på engelsk, hvor 'e' udgør 12 %, 't' udgør 9 %, 'a' 8% og 'o' godt 7 procent; 'x'', 'q', 'j' og 'z' er de bogstaver som sjældnest anvendes på engelsk.
Hvordan kunne Beale have gjort koden vanskeligere at bryde?
Der er efter min mening flere måder, så her er, hvad jeg selv ville have gjort. Det første, jeg ville have gjort, var et oversætte teksten til en andet sprog. Ekspeditionen havde (hvis vi tager pamflettens ord for givet) opholdt sig forholdsvis længe i Santa Fe, så en mulighed ville være at oversætte den til spansk, men hvis nogen bare oversatte et enkelt ord, ville de nok blive bragt på sporet; alternativt, men mere vanskeligt kunne de have lært cheyennernes sprog af de lokale indianere gennem de næsten fem år, de havde opholdt sig sammen med disse, og der anføres i brevet, at de fik hjælp til guldgraveriet af de lokale indianere. Beale har naturligvis ikke kunnet skrive cheyenne, men kan have anvendt en form for lydskrift, altså have stavet ordet som det lød. Dechifrerer man en kode og får dette ord: "hohtseesehe", vil mange nok tro, at der er noget galt med oversættelsen, men faktisk er det cheyenneordet for "januar". Har Beale så brugt denne teknik? Måske, men i givet fald har han nok brugt et mere tilgængeligt sprog, da det ville være for vanskeligt at lave en nøgle, der efter at have oversat talkoderne, også skulle kunne oversætte fra cheyenne til engelsk.
 Men
hvad kunne han (eller jeg) så have gjort. Ja, først og fremmest ville det gælde
om at lave så korte tekster, som muligt, og de tre tekster faktisk også
forholdsvis korte med B2 som den længste. Desuden ville det være vigtigt at
konstruere sin kode, så der var så få tegn, der blev gentaget som muligt. Hvis
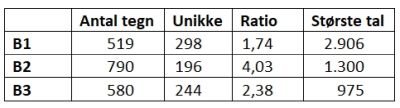
vi ser på lidt statistik over de tre koder som vist i figuren til venstre, kan
vi se, at den længste kode er B2, og selv denne tæller kun knap 800 tegn.
Kortest er B1, som er den kode, de fleste er interesserede i at få brudt, da den
jo siges at give den nøjagtige placering af skatten. Heller ikke B3 er særligt
lang, men hvad værre er, er at der er meget få gentagelser af talkoder i de
enkelte tekster; igen er der flest i B2, hvor der kun er 196 unikke tal blandt
de 790, som arket indeholder. B1 har hele 298 unikke tegn ud af 519, hvilket
svarer til en gentagelsesratio på kun 1,74 , altså under to gentagelser pr.
tegn. Det største tal, der forekommer i B1 er 2906, hvilket må betyde at denne
korte tekst måske er kodet med et forholdsvis langt dokument, hvis der er brugt samme
princip som B2, altså første bogstav i de relevante ord. Men det er nogenlunde,
det samme, jeg ville have gjort, altså lave korte tekster, med så få gentagelser
som muligt.
Men
hvad kunne han (eller jeg) så have gjort. Ja, først og fremmest ville det gælde
om at lave så korte tekster, som muligt, og de tre tekster faktisk også
forholdsvis korte med B2 som den længste. Desuden ville det være vigtigt at
konstruere sin kode, så der var så få tegn, der blev gentaget som muligt. Hvis
vi ser på lidt statistik over de tre koder som vist i figuren til venstre, kan
vi se, at den længste kode er B2, og selv denne tæller kun knap 800 tegn.
Kortest er B1, som er den kode, de fleste er interesserede i at få brudt, da den
jo siges at give den nøjagtige placering af skatten. Heller ikke B3 er særligt
lang, men hvad værre er, er at der er meget få gentagelser af talkoder i de
enkelte tekster; igen er der flest i B2, hvor der kun er 196 unikke tal blandt
de 790, som arket indeholder. B1 har hele 298 unikke tegn ud af 519, hvilket
svarer til en gentagelsesratio på kun 1,74 , altså under to gentagelser pr.
tegn. Det største tal, der forekommer i B1 er 2906, hvilket må betyde at denne
korte tekst måske er kodet med et forholdsvis langt dokument, hvis der er brugt samme
princip som B2, altså første bogstav i de relevante ord. Men det er nogenlunde,
det samme, jeg ville have gjort, altså lave korte tekster, med så få gentagelser
som muligt.
Det kan gøres på mange måder, men der er jo ingen, der siger, at man skal bruge det første bogstav i ordene. Man kunne fx bruge det sidste bogstav, det andet bogstav eller skifte mellem hvilket bogstav, man skal bruge. Som eksempel kan jeg bruge følgende: Jeg vil indkode denne korte sætning "Endnu et argument". Den vil jeg indkode med udgangspunkt i følgende tekst fra en tidligere artikel om Beale-sagen:
"Endnu et argument er, at Beales dokument B2, ikke kan dechifreres med en standardversion af Uafhængighedserklæringen, men kun af en forkortet, fejlbehæftet udgave. Til det svarer tilhængerne af skattens eksistens, at der i 1822 som omtalt oven for ikke eksisterede en standardversion, da forskellige bogtrykkere godt kunne finde på at ændre i Thomas Jeffersons ord, fx for at få dem til at "gå i svang" med den publikation, de skulle udgives i. Andre hævder, at den version, der er brugt er Jeffersons endelige udgave, og at de fejl der opstår, alle opstår omkring linjeskift". Dette skulle så igen hænge sammen med, at linjeskiftene ikke er identiske i alle versioner. Dertil kommer forklaringen ovenfor med hjælpekolonnen, hvor alle bogstaverne stod med ordene ud for, suppleret med få tællefejl."
Indkodet kommer de tre ord til at se ud som følger: 1 1 1 1 1 2 2 26 26 61 16 89 94 14 29. I denne streng er der 9 unikke tal ud af de 15, mens specielt '1' bruges mange gange - i træk. Indkodningen er sret efter dette princip: Det første bogstav skal være første bogstav i det ord, det står i. det næste bogstav skal være andet bogstav i det ord, det forekommer i. Det tredje bogstavskal være 3. bogstav og så fremdeles op til 5. Derefter startes forfra med det første bogstav i ordet igen. De første fem 1-taller repræsenterer derfor ordet "endnu", i det ettallerne repræsenter henholdsvis det første, andet, tredje, fjerde og femte bogstav i dokumentets første ord. 2 2 repræsenterer "et", idet der her er tale om det første og andet bogstav i det andet ord. Ord 26 er "svarer" - her står "a" på 3. position, i samme ord står "r" på fjerde position, i ord 61, "svang" står "g" på 5. position og så fremdeles. En sådan kode ville være vanskelig at bryde uden nøglen, men endnu sværere ville den blive, hvis der bruges en længere tekst, så 1: Det samme bogstav er ALDRIG repræsenteret ved det samme tal. 2: Tal, der går igen repræsenterer ALTID forskellige bogstaver. Koden søges bevidst konstrueret, så samme tal gentages så OFTE som muligt, men aldrig mere end i sekvenser af to, da det er meget få ord, der findes med dobbeltbogstaver og kodningen skal jo ikke i sig selv afsløre metoden.
Endnu sværere kunne det selvfølgelig gøres, hvis der til indkodningen blev brugt 3 eller fire forskellige bøger, og da Beale sandsynligvis har skrevet koderne i den periode han boede hos Morris og havde adgang til dennes tilsyneladende righoldige bibliotek, ville han dels kunne vælge blandt mange bøger, dels være sikker på at Morriss havde disse bøger, når han skulle dekode. Her kunne man måske skifte bog for hver 10 ord, for hvert ord, for hvert 25. ord eller lignende. Igen ville det ikke være vanskeligt at dechifrere, hvis man havde nøglen, men noget nær umuligt uden - specielt når man ikke vidste, hvilke bøger, der var brugt. Endnu sværere ville det være, hvis man ikke skulle bruge, de tal, der stod, men oversætte dem til andre tal (hvilket nogle af de, der hævde at de har løst koden, påstår skulle være tilfældet). Med samme princip som ovenfor, kunne de tre ord overfor komme til at se sådan ud: "2 3 3 4 4 6 10 31 52 63 48 92 376 18 145". Det første tal ganges med 2. Til det næste lægges to. Det næste ganges med 3 og til det næste lægges 3 til. Det næste ganges med 4 og så lægges 4 til. Der ganges med 5 og lægges fem til. Derefter startes forfra. Denne systematik kunne naturligvis have været gjort langt mere kompleks. Sværest bliver det selvfølgelig, hvis man bruger ord, der genererer tal, der er større end antallet af ord i det dokument, der kodes efter - hvilket kan være sket i B1, hvor der altså er brugt tal op til 2900. Hvis koden fx rummer et bredt udvalg af tal mellem 1 og 3000, vil næppe mange overveje at oversætte ved hjælp af et dokument, der kun indeholder 1000 ord.
Jeg vil også nævne muligheden for at indkode ved hjælp af dokumenter, som ikke var offentligt tilgængelige, som fx brevene fra Beale til Morris, eller en tekst, som Morriss først fik adgang til, når han skulle dekode de tre ark.
Og så kan man tænke sig kombinationer af ovenstående. Start med at generere en simpel, polyalfabetisk substitutioneskode, fx med fem alfabeter, som nogen mener at Beale har gjort. De bogstaver, der kommer ud af denne, oversættes så til tal, ved hjælp af en antal tilgængelige bøger og efter et system, hvor det ikke altid er første bogstav, der skal bruges, men andre bogstaver efter et system, som kun Beale og Morriss kendte. Evt. kunne man bruge hele ord fra et eller flere af dokumenterne og enkeltbogstaver fra andre. Er der brugt hele ord fra et enkelt eller flere dokumenter og ikke bogstaver, kan det forklare, hvordan det forholdsvis korte B3, kan indeholde navne, adresser og efterkommere på 30 personer. Af andre måder at vanskeliggøre oversættelsen på, kan nævnes at man bevidst laver "stavefjel" i nogle ord i orignalteksten, bevidst lavet (få) tællefejl, når der indkodes fra bøgerne, at man indsætter tilfældige bogstaver hist og her i ordene, eller indsætter irrelevante eller ligefrem volapykord af og til. Her er en tekst fra en bog, jeg har skrevet:
"We found a new place in a modern office building, not far from the old place, and rented a larger office, where there is room for further expansion. So about one month ago, we started to pack everything in boxes in order to be ready for our move. One afternoon my secretary entered my office, carrying a thick, brown and dusty envelope in her hand."
Inden jeg begynder at kode, ændrer jeg teksten til:
"Ve foond a new place in a justfun moder ofice bilding, not far ikkek from the old plac, and rented a lager janjan office, where there is roum for further blanket expansion. So about one montch ago, we started to pak everything in bokses in order to be ready for our move church. One afternoon my sekretary enkered my office, carrying a elehpant and zebrathick, brown and dusty envelop in her hand. "
som nok ser mærkelig ud, men som sagtens kan forstås. Denne tekst koder jeg nu med en polyalabetisk kode baseret på (for eksemplets skyld) to alafabeter, hvor jeg ville anbefale fem eller flere. Her skifter jeg alfabet for hvert ord, men jeg kunne have skiftet på en anden måde:
bkraazpgzqivrgikuzavgefrgzsujkxaruoqhorjotmzaflgxoqqkqrdayznkaxpvrgimzpxktzkjgxmsqdpgtpgtarruoqcnkxkftqdqoydagyluxrgdftqdhrgtqkzqjbmzeuazyumnagfutkyazfotgmuiqyzgxzkpfavgqqh-
qdkftuzsotnaweqeotadpqdzunqxkgjeraduaxyahqinaxnazqglzkxtuutykykixkzgxeqzwqdqpsearruoqigxxeotmmkrknvgtzmzpfkhxgznoiqndaizgtjpgefkktbkruvuznkxtmzp
og det er nu denne tekst, der skal omsættes til tal. For ikke at bruge for meget tid på denne, egentlige ret ligegyldige kode, har jeg valgt kun at "oversætte" de fem første ord. Disse oversættes med to forskellige bøger og et privat dokument. Der skiftes bog for hvert tredje bogstav. Det jeg vil "oversætte" er således "bkraazpgzqivrgik". Jeg har valgt at oversætte med to engelsksprogede bøger, men kunne have valgt dansksprogede for at gøre det endnu mere vanskeligt - altså bøger på et sprog, der er fremmed i forhold til den tekst, der skal oversættes. Havde jeg valgt at oversætte den engelske tekst til et fremmedsprog, kunne jeg fx have valgt tysk og så bruge franske bøger til indkodningen. De bøger jeg har valgt her er 'True Evil' af Greg Iles og 'The Guilt of Innocents' af Candace Robb; ingen af dem eksisterede på Beales tid, men de stod tilfældigvis i min bogreol. Desuden har jeg brugt et privat dokument, skrevet på engelsk, for ikke at forvirre for meget ved sprogblanding, hvilket ikke ville være en hindring, hvis jeg faktisk skulle kamuflere en kode. De tal, der er kommet ud af min indkodning er:
332243,231774,711459,495566,316447,862573,266249,901974,441945,602923,965293,821777,521479,312566,852477,771281
hvoraf det fremgår, at jeg arbejder i grupper af seks cifre pr. bogstav, men det kunne modtager jo vide som en del af nøglen, og så kunne tallene bare se sådan ud
332243231774711459495566316447862573266249901974441945602923965293821777521479312566852477771281
Man kunne også vælge at dele tallene op tilfældigt, så de lignede ord i en sætning eller dele dem op i grupper af to, tre og fire
33 2243 231 774711 459495 566 31 6447 8625 73266 249 901 97444 1945 60 2923 9652 938217 7752 147 931 256685 24777 7 1281 eller
322 432 317 747 114 594 955 663 1644 786 257 326 624 990 1974 441 945 602 923 965 293 82 1777 521 47 931 25 668 52 47 777 1281
Det ville medvirke til at forvirre en person, men nok ikke en computer. Hvordan er jeg så nået frem til disse tal? I stedet for at tælle ord i dokumenterne, hvilket ville tage for lang tid i forhold til denne artikel, men ikke i forhold til Beale, som havde flere måneder til sin rådighed, har jeg valgt at lade tallene repræsentere sidenummer, linjenummer på siden, nummeret af ord i linjen og endelig bogstav i ordet. Er side eller linjenummer eller begge mindre end 2-cifret, tilføjer jeg 0'er i slutningen af tallet for at få en fast længde på seks. Det vil sige, at jeg kan få tal som 495420 eller 316300. I sidste tilfælde er både side og linje under 10 (hvilket man selvfølgelig kunne undgå ved altid at vælge sider og linjer større end 10). Til gengæld er der aldrig valgt ord aller bogstav i ord, der er større end 9. En indvending kunne være, at hvis der kun er et 0 til sidst, kan det være både side eller linje, der er mindre end 10, hvilket er korrekt. Her må den der skal dechifrere så prøve hvilken af mulighederne, der passer. For ikke at gøre systemet med 0'erne til sidst for åbenlyst, har jeg valgt at lægge 143 til det første tal, 144 til det næste og så fremdeles, hvilket er årsagen til at ingen af grupperne med de sekes cifre faktisk slutter med 0.
Kan denne kode så ikke brydes? Formodentlig ikke af en person uden nøglen, som er jo er ret kompleks. Af en computer? Måske, men det ville tage nogen tid selv for en hurtig computer, og ville nok være umuligt, hvis teksten var kort.
Her er det brev, jeg ville skrive til modtageren (det brev Morriss aldrig fik)
Kære Morris
For at dechifrere koden, skal du først dele alle tallene op i grupper af seks. Så skal du trækker 143 fra den første gruppe, 144 fra den næste og så fremdeles. De tal, du nu har, referer til sider, linjer, ord og bogstav i ordet i de to bøger, vi diskuterede under mit ophold, Greg Iles, True Evil og Candace Robb, The Guilt of Innocents, foruden det manuskript, du fik af mig inden jeg rejste. For hvert tredje ord skal du skifte kilde. Prøv dig from med de første ord for at finde ud af, i hvilken rækkefølge du skal bruge kilderne. Hvis et tal slutter med et to 0'er, er det fordi side- og linjenummer er mindre end 10. Slutter det med et enkelt 0, er kun en af delene mindre end 10, og her må du derfor prøve begge versioner, for at se, hvad der giver mening.
Du når nu frem til en række bogstaver, der kan se tilfældige ud, men det er faktisk en underliggende kode bestående af to alfabeter, som skifter for hvert ord. Disse to alfabeter kan du finde på et stykke papir, som jeg gemte i dit eksemplar af Decaameron inden jeg tog af sted. Oversæt teksten med disse to alfabeter og du når frem til en tekst, der måske stadig ser lidt mystisk ud, men det er fordi, jeg dels har lavet bevidste stavefjel, dels har tilføjet meningsløse ord rundt omkring. Det er jeg sikker på at du nok skal gennemskue.
Dette vil være det sidste, du hører fra mig
Thomas J. Beale
Og det var måske et sådant brev, som aldrig nåede frem til Robertt Morriss i 1832.